Při řešení úloh ve vyšší matematice vzniká potřeba velmi často vypočítat determinant matice. Determinant matice se objevuje v lineární algebře, analytické geometrii, matematické analýze a dalších odvětvích vyšší matematiky. Bez dovednosti řešit determinanty se tedy jednoduše neobejdete. Pro vlastní testování si také můžete zdarma stáhnout kalkulačku determinantů, která vás sama o sobě nenaučí řešit determinanty, ale je to velmi pohodlné, protože je vždy výhodné znát správnou odpověď předem!
Nebudu uvádět striktní matematickou definici determinantu a obecně se pokusím minimalizovat matematickou terminologii, což většině čtenářů neusnadní. Účelem tohoto článku je naučit vás řešit determinanty druhého, třetího a čtvrtého řádu. Veškerý materiál je prezentován v jednoduché a přístupné formě a dokonce i plná (prázdná) konvice ve vyšší matematice po pečlivém prostudování materiálu bude schopna správně vyřešit determinanty.
Determinant lze vypočítat pouze pro čtvercovou matici (další podrobnosti viz Akce s maticemi)
V praxi se můžete nejčastěji setkat s determinantem druhého řádu, např.: , a determinantem třetího řádu, např.: .
Determinant čtvrtého řádu také není starožitnost a přijdeme k němu na konci lekce.
Doufám, že každý pochopí následující: Čísla uvnitř determinantu žijí sama o sobě a o nějakém odčítání nemůže být řeč! Čísla nelze zaměnit!
(Především je možné provádět párové přeskupení řádků nebo sloupců determinantu se změnou jeho znaménka, ale často to není nutné – viz další lekce Vlastnosti determinantu a snížení jeho pořadí)
Pokud je tedy dán nějaký determinant, pak Nedotýkáme se ničeho uvnitř!
Zápis: Pokud je dána matice, pak její determinant je označen . Velmi často se determinant označuje latinkou nebo řečtinou.
1) Co to znamená vyřešit (najít, odhalit) determinant? Vypočítat determinant znamená NAJÍT ČÍSLO. Otazníky ve výše uvedených příkladech jsou úplně obyčejná čísla.
2) Teď zbývá přijít na to JAK toto číslo zjistit? Chcete-li to provést, musíte použít určitá pravidla, vzorce a algoritmy, o kterých se nyní bude diskutovat.
Začněme s determinantem “dva” po “dvě”:
TOTO JE NUTNÉ SI ZAPAMATOVAT alespoň při studiu vyšší matematiky na vysoké škole.
Podívejme se hned na příklad:
Připraveno. Nejdůležitější je NESMÍT SE VE ZNAMENÍCH.
Determinant matice tři krát tři lze otevřít 8 způsoby, z toho 2 jednoduché a 6 normálních.
Začněme dvěma jednoduchými způsoby
Podobně jako u determinantu dva na dva lze determinant tři na tři rozšířit pomocí vzorce:
Vzorec je dlouhý a je snadné udělat chybu kvůli neopatrnosti. Jak se vyhnout nepříjemným chybám? Za tímto účelem byl vynalezen druhý způsob výpočtu determinantu, který se vlastně shoduje s prvním. Říká se tomu Sarrusova metoda nebo metoda „paralelních pásů“.
Spodní řádek je ten, že napravo od determinantu přiřaďte první a druhý sloupec a pečlivě nakreslete čáry tužkou:
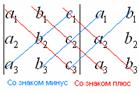
Násobiče umístěné na „červených“ úhlopříčkách jsou ve vzorci zahrnuty se znaménkem „plus“.
Násobiče umístěné na „modrých“ úhlopříčkách jsou ve vzorci zahrnuty se znaménkem mínus:
Porovnejte obě řešení. Je snadné vidět, že jde o STEJNOU věc, akorát ve druhém případě jsou faktory vzorce mírně přeskupeny, a co je nejdůležitější, pravděpodobnost, že uděláte chybu, je mnohem menší.
Nyní se podíváme na šest normálních způsobů výpočtu determinantu
Proč normální? Protože v drtivé většině případů je třeba kvalifikanty takto zveřejňovat.
Jak jste si všimli, determinant tři krát tři má tři sloupce a tři řádky.
Determinant můžete vyřešit jeho otevřením podle libovolného řádku nebo libovolného sloupce.
Existuje tedy 6 metod, které se ve všech případech používají stejný typ algoritmus.
Determinant matice se rovná součtu součinů prvků řádku (sloupce) odpovídajícími algebraickými doplňky. děsivé? Vše je mnohem jednodušší, použijeme nevědecký, ale srozumitelný přístup, přístupný i člověku daleko od matematiky.
V dalším příkladu rozšíříme determinant na prvním řádku.
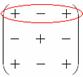
K tomu potřebujeme matici znaků: . Je snadné si všimnout, že znaky jsou uspořádány do šachovnicového vzoru.
Pozornost! Znaková matice je můj vlastní vynález. Tento koncept není vědecký, není nutné jej používat při konečném návrhu zadání, pouze vám pomůže pochopit algoritmus pro výpočet determinantu.
Nejprve uvedu kompletní řešení. Znovu vezmeme náš experimentální determinant a provedeme výpočty:
A hlavní otázka: JAK to získat z determinantu „tři na tři“:
?
Takže determinant „tři na tři“ spočívá v řešení tří malých determinantů, nebo jak se jim také říká, MINOROV. Doporučuji si zapamatovat termín, zejména proto, že je zapamatovatelný: vedlejší – malý.
Jakmile je zvolena metoda rozkladu determinantu na prvním řádku, je zřejmé, že se vše točí kolem ní: 
Prvky se obvykle zobrazují zleva doprava (nebo shora dolů, pokud byl vybrán sloupec)
Pojďme, nejprve se zabýváme prvním prvkem řádku, tedy jedním:

1) Z matice znaků vypíšeme odpovídající znak:
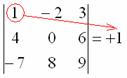
2) Poté zapíšeme samotný prvek:
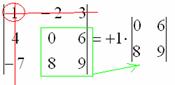
3) V MÉNĚ přeškrtněte řádek a sloupec, ve kterém se vyskytuje první prvek:
Zbývající čtyři čísla tvoří determinant „dva po dvou“, který se nazývá MÉNĚ DŮLEŽITÝ daného prvku (jednotky).
Přejdeme k druhému prvku řádku.
4) Z matice znaků vypíšeme odpovídající znak:
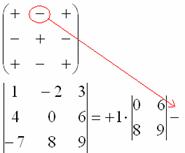
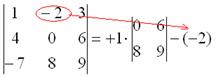
5) Poté napište druhý prvek:
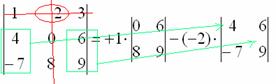
6) V PŮSOBNOSTI škrtněte řádek a sloupec, ve kterém se vyskytuje druhý prvek:
Zbývající čtyři čísla zapíšeme malým determinantem.
No, třetí prvek prvního řádku. Žádná originalita:
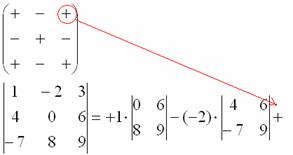
7) Z matice znaků vypíšeme odpovídající znak:
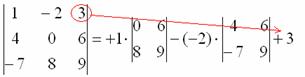
8) Napište třetí prvek:
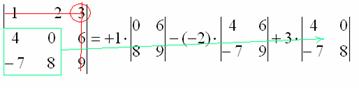
9) V MÉNĚ přeškrtněte řádek a sloupec, který obsahuje třetí prvek:
Zbývající čtyři čísla zapíšeme malým determinantem.
Zbývající akce nepředstavují žádné potíže, protože již víme, jak počítat determinanty dva krát dva. NENECHTE SE ZMÝTIT VE ZNAMENÍCH!
Podobně lze determinant rozšířit přes libovolný řádek nebo do libovolného sloupce. Přirozeně je ve všech šesti případech odpověď stejná.
Pomocí stejného algoritmu lze vypočítat determinant čtyři krát čtyři.
V tomto případě se naše matice znaků zvýší:
V následujícím příkladu jsem rozšířil determinant podle čtvrtého sloupce:
Jak se to stalo, zkuste na to přijít sami. Další informace přijdou později. Pokud chce někdo řešit determinant až do konce, správná odpověď je: 18. Pro procvičení je lepší řešit determinant nějakým jiným sloupcem nebo jiným řádkem.
Procvičování, odkrývání, provádění výpočtů je velmi dobré a užitečné. Ale kolik času strávíte na velké kvalifikaci? Neexistuje rychlejší a spolehlivější způsob? Doporučuji vám seznámit se s efektivními metodami výpočtu determinantů ve druhé lekci – Vlastnosti determinantu. Snížení pořadí determinantu.
Autor: Emelin Alexander


(Přejít na hlavní stránku)

Zaochnik.com – odborná pomoc pro studenty,
15% sleva na vaši první objednávku, zadejte propagační kód při pokladně: 5530-hihi5
© Copyright mathprofi.ru, Alexander Emelin, 2010-2023. Kopírování materiálů stránek je zakázáno
Co je vedlejší a algebraický doplněk matice
Vedlejší Mij k prvku aij determinantu n-tého řádu je determinant (n−1)-tého řádu získaný z počátečního determinantu po odstranění i-tého řádku a j-tého sloupce.
Na základě definice je vedlejší determinant, který zůstává po přeškrtnutí konkrétního řádku a konkrétního sloupce. Například M12 by bylo získáno odstraněním prvního řádku a druhého sloupce. Chcete-li získat M34, přeškrtněte třetí řádek a čtvrtý sloupec.
Nezletilé můžete najít pomocí přeškrtnutí podle následujícího algoritmu:
Opatrně! Pokud učitel v práci odhalí plagiát, nelze se vyhnout velkým problémům (až vyloučení). Pokud nemůžete napsat sami, objednejte zde.
- odstranění i-tého řádku;
- přeškrtnout j-tý sloupec;
- záznam determinantu, který byl získán jako výsledek provedených manipulací.
Algebraický doplněk Aij k prvku aij determinantu n-tého řádu je číslo (A_=(-1)^Mij), ve kterém i, j jsou odpovídající řádek a sloupec a Mij je vedlejší prvek příslušného prvku. .
Postup pro určení algebraického doplňku je následující:
- určení součtu čísel řádků (i) a sloupců (j);
- vyhledání nezletilé Mij pomocí algoritmu pro výpočet nezletilých, který byl popsán výše;
- dosazením hodnot, které byly získány v první a druhé fázi výpočtu, do vzorce (A_=(-1)^Mij.)
Obecné pojmy, základní vzorce
Předpokládejme, že existuje nějaký druh čtvercové matice nebo čtvercové matice n-tého řádu:
(Minor M_ prvku a_ matice A_) bude determinant matice, který se získá z matice A v důsledku eliminace i-tého řádku a j-tého sloupce, které jsou umístěny tak, že se jejich průsečík shoduje s prvkem (a_.)
Jako důkaz můžeme považovat následující čtvercovou matici čtvrtého řádu:
(A=vlevo( začátek 1 & 0 & -3 & 9 2 & -7 & 11 & 5 -9 & 4 & 25 & 84 3 & 12 & -5 & 58 konec vpravo))
Pro prvek (a_) je nutné definovat minor, tedy (M_) . Nejprve byste si měli zapsat moll (M_) a poté jej vypočítat. Postup pro skládání (M_) zahrnuje odstranění třetího řádku a druhého sloupce z matice A. Tato akce je způsobena skutečností, že prvek (a_) je umístěn v místě, kde se protíná třetí řádek a druhý sloupec. Tak byla získána nová matice s determinantem ve formě požadovaného minoru (M_).
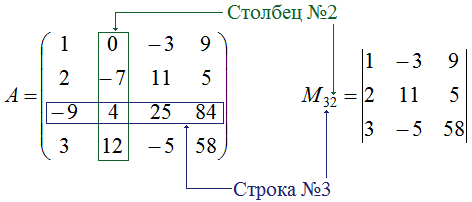
Tuto minoritu lze snadno vypočítat pomocí věty pro výpočet determinantů druhého a třetího řádu. Výpočet bude následující:
(M_=levý| začátek 1 & -3 & 9 2 & 11 & 5 3 & -5 & 58 konec vpravo|= 1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11 cdot 3-(-3) cdot 2cdot 58-5cdot (-5)cdot 1=579)
Menší hodnota prvku (a_) je tedy 579, tedy (M_=579)
V odborné literatuře se často místo „vedlejšího prvku matice“ používá pojem „vedlejší prvek determinantu“. Význam výrazu je zachován. Pro výpočet moll prvku (a_) je tedy nutné vyloučit i-tý řádek a j-tý sloupec z počátečního determinantu. Prvky, které zůstanou, by měly být zapsány do nového determinantu, kterým je vedlejší prvek prvku (a_.)
Jako příklad můžeme vypočítat vedlejší prvek (a_) determinantu:
(vlevo| začátek -1 & 3 & 2 9 & 0 & -5 4 & -3 & 7 konec vpravo|)
Nejprve si musíte zapsat požadovanou moll (M_). Chcete-li to provést, můžete z daného determinantu vyloučit první řádek a druhý sloupec:
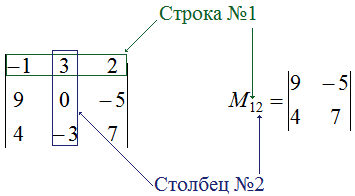
Doporučuje se vypočítat minor pomocí vzorce pro výpočet determinantů druhého a třetího řádu:
(M_=vlevo| začátek 9 & -5 4 & 7 konec vpravo|=9cdot 7-(-5)cdot 4=83)
Výsledkem je, že vedlejší prvek (a_) bude 83, tedy (M_=83)
Předpokládejme, že existuje nějaký druh čtvercové matice (A_), tedy čtvercová matice n-tého řádu. Algebraický doplněk (A_) prvku (a_) matice (A_) lze určit pomocí vzorce:
kde (M_) je minorita prvku (a_.)
Jako příklad můžeme vypočítat algebraický doplněk prvku (a_) matice:
(A=vlevo( začátek 1 & 0 & -3 & 9 2 & -7 & 11 & 5 -9 & 4 & 25 & 84 3 & 12 & -5 & 58 konec vpravo))
V důsledku toho musíte získat hodnotu pro (A_) . V předchozím příkladu již byl výpočet pro vedlejší (M_=579), takže je vhodné v tomto problému použít dostupná data:
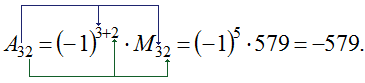
Obvykle při definování algebraických doplňků není nutné provádět samostatný výpočet vedlejšího před vyhodnocením samotného doplňku. Pokud například chcete určit (A_) za předpokladu, že:
(A=left( začátek -5 & 10 & 2 6 & 9 & -4 4 & -3 & 1 konec vpravo))
Je nutné zapsat spravedlivou rovnost:
Je snadné vypočítat (M_) přeškrtnutím prvního řádku a druhého sloupce matice A. Není tedy potřeba zavádět extra zápis pro moll. Stačí rovnou zapsat rovnici pro algebraický doplněk (A_):
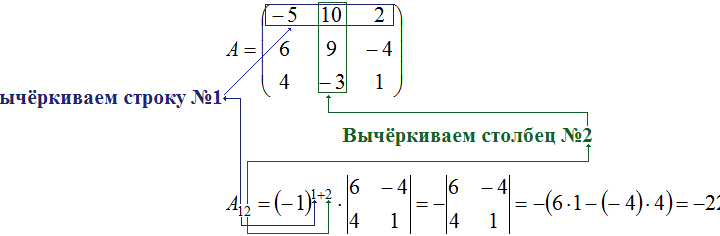
Řešení mollů a algebraických sčítání
Vedlejší a algebraické doplňky se vyskytují v úlohách nejen se čtvercovými maticemi, ale také s pravoúhlými. V tom druhém se matice liší počet řádků nemusí být nutně stejný jako počet sloupců. Například matice je napsána:
Dotyčná matice má m řádků a n sloupců. K-tý řád matice (A_) je determinant s prvky umístěnými v průsečíku k řádků a k sloupců matice A. Je třeba vzít v úvahu, že v tomto případě k≤ ma k≤ n.
Jako příklad zvažte matici:
(A=vlevo( začátek -1 & 0 & -3 & 9 2 & 7 & 14 & 6 15 & -27 & 18 & 31 0 & 1 & 19 & 8 0 & -12 & 20 & 14 5 & 3 & -21 & 9 23 & -10 & -5 & 58 konec vpravo))
Můžete k tomu napsat nějaký druh moll třetího řádu. Chcete-li to provést, měli byste vybrat tři řádky a tři sloupce příslušné matice. Vyberme pro výpočet řádky č. 2, č. 4, č. 6 a sloupce č. 1, č. 2, č. 4. Tyto řádky a sloupce se budou protínat v místě, kde se nacházejí prvky požadované vedlejší položky.
(M=left|začátek 2 & 7 & 6 0 & 1 & 8 5 & 3 & 9 konec vpravo|.)
Uspořádání nezletilých prvního řádu se bude shodovat s průsečíkem jednoho řádku a jednoho sloupce. Odvodíme tedy rovnost minorů prvního řádu k prvkům uvažované matice.
K-tý řád matice (A_=(a_)) je klíčový v případě, kdy hlavní diagonála dané vedlejší obsahuje výhradně klíčové diagonální prvky matice A.
Hlavní diagonální prvky jsou ty prvky matice, které obsahují indexy rovné ( a_, a_, a_) a tak dále. Například matice A, která je uvažována v příkladu, obsahuje prvky (a_=-1, a_=7, a_=18, a_=8.)
(vlevo( začátek & 0 & -3 & 9 2 & & 14 & 6 15 & -27 & & 31 0 & 1 & 19 & 0 & -12 & 20 & 14 5 & 3 & -21 & 9 23 & -10 & -5 & 58 konec vpravo))
V případě, že jsou v matici A vyloučeny řádky a sloupce, které odpovídají číslům 1 a 3, bude jejich průsečík splývat s prvky druhého řádu moll. Hlavní úhlopříčka této vedlejší bude obsahovat pouze diagonální prvky matice A. Takovými prvky jsou například prvky (a_=-1) a (a_=18) matice A. Hlavní vedlejší matice matice A objednávka se bude rovnat:
V takovém případě, pokud vyberete řádky a sloupce s různými čísly, získáte další durovou moll druhého řádu.
Můžeme předpokládat, že nějaký vedlejší M k-tého řádu matice A_ má nenulovou hodnotu, tedy Mneq 0. V tomto případě platí pro všechny minory s řády vyššími než k rovnost nule. Potom je vedlejší M základní a řádky a sloupce obsahující prvky základního mollového se nazývají základní řádky a základní sloupce.
Jako příklad zvažte následující matici:
(A=left( začátek -1 & 0 & 3 & 0 & 0 2 & 0 & 4 & 1 & 0 1 & 0 & -2 & -1 & 0 0 & 0 & 0 & 0 & 0 konec vpravo ))
Zápis moll uvažované matice s prvky umístěnými v místě, kde se protínají řádky č. 1, č. 2, č. 3 a sloupce č. 1, č. 3, č. 4, je moll třetího řádu a má následující podobu:
(; M=left|začátek -1 & 3 & 0 2 & 4 & 1 1 & -2 & -1 konec vpravo|)
Hodnotu požadovaného minoru můžete vypočítat pomocí pravidla pro výpočet determinantů druhého a třetího řádu:
(M=vlevo| začátek -1 & 3 & 0 2 & 4 & 1 1 & -2 & -1 konec vpravo|=4+3+6-2=11)
Dále si můžete zkusit zapsat libovolný moll s řádem vyšším než 3. K sestavení moll čtvrtého řádu je třeba použít čtvrtý řádek, jehož prvky mají nulové hodnoty. Na základě toho můžeme usoudit, že jakýkoli moll čtvrtého řádu má nulový řádek. Hodnota každého z nezletilých čtvrtého řádu je tedy nulová. Z důvodu přítomnosti pouze čtyř řádků v matici A není možné psát nezletilé pátého řádu a vyššího.
Na základě výsledků výpočtu bylo možné určit nezletilého třetího řádu s nenulovou hodnotou. Nezletilí vyšších řádů se přitom rovnají nule, z čehož můžeme usoudit: dotyčný nezletilý je základní. Řádky č. 1, č. 2, č. 3 matice A, které obsahují prvky dané vedlejší, jsou základními řádky a sloupce č. 1, č. 3, č. 4 matice A jsou základními sloupci.
Uvedený příklad je triviální. S jeho pomocí je však vhodné demonstrovat význam základní moll. V reálných podmínkách může existovat více než jeden základ nezletilých a řešení podobných problémů k nalezení takového nezletilého je mnohem složitější a rozsáhlejší.
Dalším důležitým pojmem je okrajová moll. Pro vysvětlení pojmu můžeme předpokládat, že nějaký moll k-tého řádu M matice (A_) se nachází v místě, kde se protíná k řádků a k sloupců. Pokud k množině daných řádků a sloupců přidáme další řádek a sloupec, pak výsledný (k+1) moll řádu je hraniční moll pro vedlejší M.
Jako příklad zvažte matici:
(A=left( začátek -1 & 2 & 0 & -2 & -14 3 & -17 & -3 & 19 & 29 5 & -6 & 8 & -9 & 41 -5 & 11 & 19 & -20 & -98 6 & 12 & 20 & 21 & 54 -7 & 10 & 14 & -36 & 79 konec vpravo))
Nejprve je potřeba zapsat moll 2. řádu s prvky umístěnými v místě, kde se protínají řádky č. 5 a č. 2 a také sloupce č. 4 a č. XNUMX.
(M=left|začátek -17 & 19 12 & 21 konec vpravo|)
K množině řádků s prvky vedlejší M je třeba přidat jeden řádek č. 1 a ke sloupcům – sloupec č. 5. V důsledku manipulací bude získáno nové moll M‘ třetího řádu s prvky umístěnými v místech, kde se protínají řádky č. 1, č. 2, č. 5 a sloupce č. 2, č. 4, č. 5.
(M’=left|začátek 2 & -2 & -14 -17 & 19 & 29 12 & 21 & 54 konec vpravo|)
Vedlejší M’ je hraniční moll pro malé M. Stejně tak přidáním řádku č. 4 do množiny řádků s prvky vedlejšího M a sloupce č. 3 do množiny sloupců můžeme zapsat moll M“, tedy moll třetího řádu.
( M»=vlevo|začátek -17 & -3 & 19 11 & 19 & -20 12 & 20 & 21 konec vpravo|.)
moll M“, podobně jako předchozí, je pro moll M hraniční moll.
Předpokládejme, že existuje nějaké vedlejší M k-tého řádu matice (A_.)
Determinant (n-k)-tého řádu s prvky získanými z matice A eliminací řádků a sloupců, které obsahovaly vedlejší M, se nazývá komplementární moll k vedlejší M.
Jako příklad uvažujme čtvercovou matici pátého řádu:
(A=left( začátek -1 & 2 & 0 & -2 & -14 3 & -17 & -3 & 19 & 29 5 & -6 & 8 & -9 & 41 -5 & 11 & 16 & -20 & -98 -7 & 10 & 14 & -36 & 79 konec vpravo))
V uvažované matici můžete vybrat řádky č. 1 a č. 3, sloupce č. 2 a č. 5. Průsečík těchto řádků a sloupců se bude shodovat s prvky vedlejšího M druhého řádu.
( M=left|začátek 2 & -14 -6 & 41 konec vpravo|)
Dále by měly být z matice A vyloučeny řádky č. 1 a č. 3 a také sloupce č. 2 a č. 5. V průsečíku těchto složek jsou prvky vedlejšího M. Prvky, které zůstanou nedotčeny, budou tvořit vedlejší M’.
(M’=left|začátek 3 & -3 & 19 -5 & 16 & -20 -7 & 14 & -36 endright|)
Vedlejší M’ s pořadím odpovídajícím 5-2=3 je moll, který je komplementární k mollovému M.
Algebraický doplněk k malému M čtvercové matice (A_) se zapisuje takto:
V tomto případě je alfa součet čísel řádků a sloupců matice A obsahující prvky vedlejšího M a M’ je doplněk vedlejšího M. Termín „algebraický doplněk k vedlejšímu M“ se obvykle formuluje takto: „algebraický doplněk vedlejšího M“.
Jako příklad můžeme uvažovat matici A. Dříve byla pro uvažovanou matici při výpočtech určena minorita druhého řádu:
(M=vlevo| začátek 2 & -14 -6 & 41 konec vpravo|)
Kromě této nezletilé osoby je tato nezletilá třetího řádu:
(M’=left| začátek 3 & -3 & 19 -5 & 16 & -20 -7 & 14 & -36 konec vpravo|)
Jako označení pro algebraický doplněk vedlejšího M je vhodné použít: M^*
Na základě definice dostaneme:
Parametr alfa je součtem čísel řádků a sloupců, které odpovídají vedlejšímu M. Umístění této vedlejší položky odpovídá průsečíku řádků č. 1, č. 3 a sloupců č. 2, č. 5. Tím pádem:
V důsledku toho můžeme napsat:
(M^*=(-1)^cdot M’=-vlevo| začátek 3 & -3 & 19 -5 & 16 & -20 -7 & 14 & -36 konec vpravo|)
Díky vzorci pro výpočet determinantů druhého a třetího řádu je možné vypočítat algebraický doplněk:
(M^*=-vlevo| začátek 3 & -3 & 19 -5 & 16 & -20 -7 & 14 & -36 konec vpravo|=-30)
















