Tento přírodní jev se snažili vysvětlit vědci z různých dob. Kompletní teorie duhy přesahuje geometrickou a dokonce vlnovou optiku a vyžaduje výkonný matematický aparát. Film dává první představu o duze, která je však úžasná a v žádném případě jednoduchá. Tato myšlenka je založena na díle René Descartes a Isaac Newton.
René Descartes vysvětlil geometrii duhy: její tvar a umístění na obloze. Isaac Newton „obarvil“ duhu a vysvětlil její barvy.
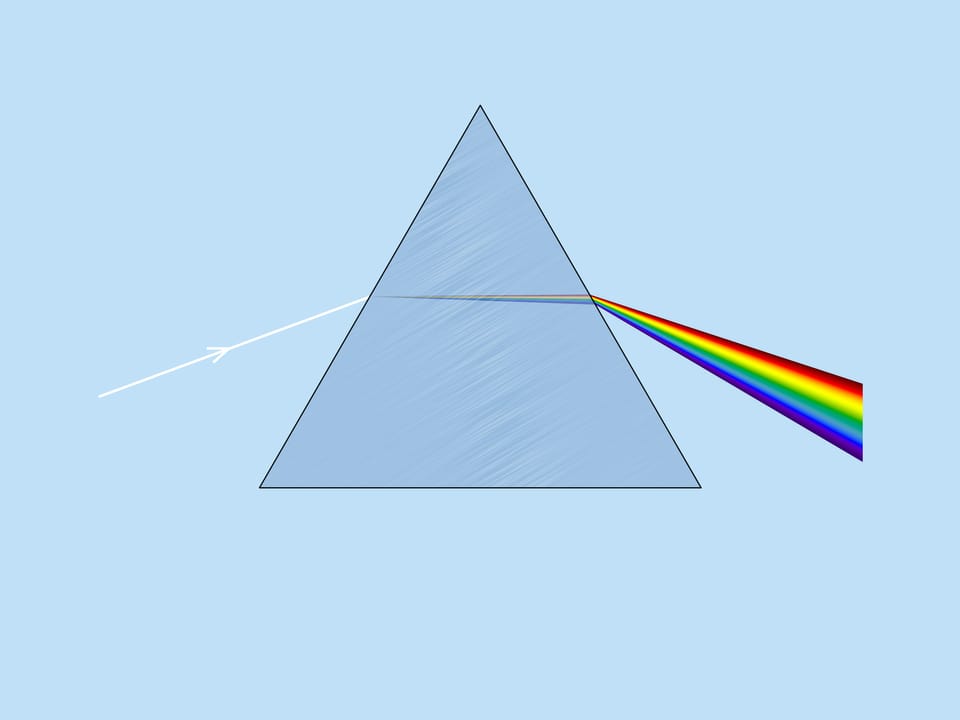
Velký Isaac Newton ve svém slavném experimentu se skleněným hranolem, bez kterého jsou dnes hodiny fyziky nepostradatelné, rozložil bílé sluneční světlo na barevné složky a ukázal, že různé barvy odpovídají různým indexům lomu. Tento jev se nazývá rozptyl světla. Právě díky disperzi je duha vícebarevná.
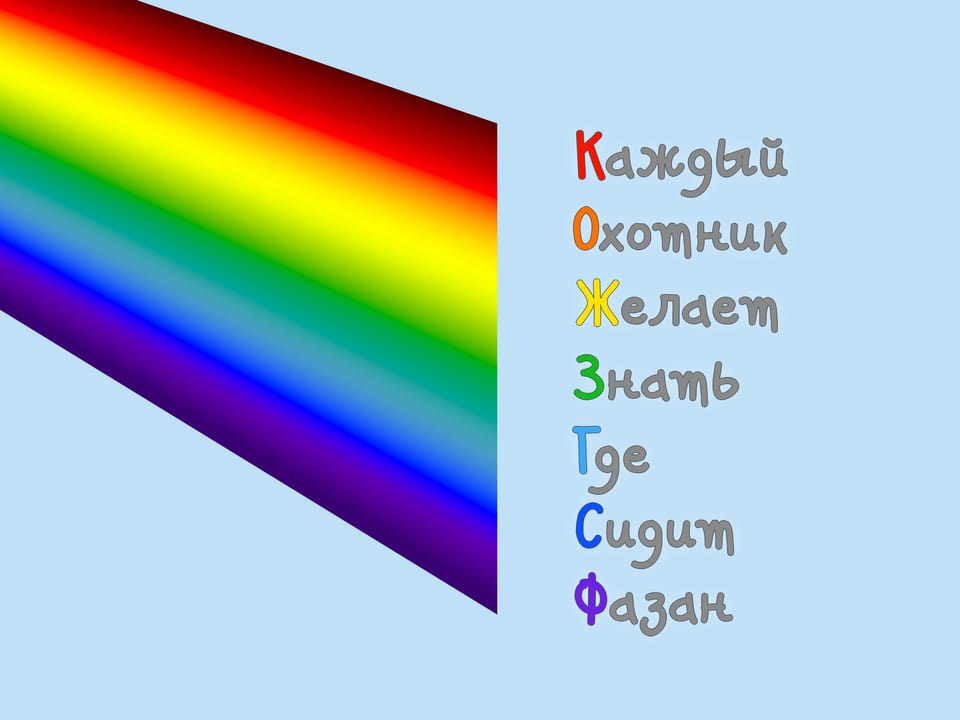
Ve výsledném spektru jsem identifikoval sedm složek: červenou, oranžovou, žlutou, zelenou, modrou, indigovou, fialovou. Tyto barvy jsou snadno zapamatovatelné pomocí známé mnemotechnické pomůcky „Každý lovec chce vědět, kde bažant sedí“. Zajímavé je, že ne všechny země uznávají sedm barev duhy. Například v Japonsku – šest.

Duhy se tvoří ve vzdušných dešťových kapkách. Abyste přesně pochopili, jak se to děje, zvažte dráhu slunečního světla v jedné kapce vody. Budeme předpokládat, že kapka má tvar koule. (Rene Descartes provedl tisíce experimentů se skleněnou kulovou baňkou naplněnou vodou.) Díky symetrii závisí dráha paprsku v kapce pouze na jeho vzdálenosti od středu kapky. Uvažujme paprsky, které leží v rovině „Slunce – oko pozorovatele – střed kapky“.
Protože se Slunce nachází velmi daleko od Země, můžeme předpokládat, že paprsky z něj dopadají do zemské atmosféry vzájemně rovnoběžně a úhel jejich dopadu závisí pouze na výšce Slunce nad obzorem.
Sluneční paprsky, které tvoří duhu, vstupují do kapky ze vzduchu a poté vycházejí, přičemž dochází k řadě lomů a odrazů. Na rozhraní dvou prostředí, v tomto případě vody a vzduchu, dochází vždy k lomu i odrazu. Budeme uvažovat pouze takový průběh paprsků, který je zajímavý z hlediska vzniku duhy.
Podívejme se nejprve na ty paprsky, které dopadly na horní polovinu kapky. Při vstupu do kapky se tyto paprsky lámou, poté se odrážejí od zadní stěny kapky a znovu lámané vycházejí ven. Když dojde k lomu, dojde k disperzi a objeví se barvy.
Paprsky dopadají rovnoměrně na povrch kapky obrácený ke Slunci. Při výstupu z kapky jsou již paprsky rozloženy nerovnoměrně. Pojďme zjistit, které paprsky se objeví a vytvoří duhu.



Paprsek, který dopadne na kapku přesně ve středu, se neláme (protože úhel dopadu je $0^$). Po odrazu od zadního povrchu kapky vyjde směrem k dopadajícímu paprsku. Paprsky, které dopadnou na kapku blízko středu, se příliš nelámou (protože jejich úhel dopadu je blízko $0^$). Po odrazu tyto paprsky vycházejí téměř směrem k dopadajícím, přičemž se odchylují od návratu opačným směrem o malý úhel. Jak se přicházející paprsky vzdalují od středu kapky, tento úhel se zvětšuje, ale v určitém bodě je dosaženo maxima: paprsky nacházející se přibližně $086$ poloměru kapky od středu jsou odkloněny nejvíce. S větší vzdáleností od středu kapky dolů k těm paprskům, které se kapky pouze dotýkají, se úhel zmenšuje.




U červených paprsků se předpokládalo, že index lomu ve filmu je roven $textit$, což odpovídá skutečnosti. U všech ostatních barev byly pro větší přehlednost koeficienty mírně zvýšeny oproti skutečným.
V blízkosti maximální (matematici říkají extrémní) hodnoty se úhel vychýlení mění pomalu, takže dochází k „akumulaci“ vznikajících paprsků. Právě tyto paprsky jsou vnímány jako duha.
Jak již bylo zmíněno, index lomu pro paprsky různých barev je odlišný, takže i maximální úhel vychýlení je odlišný. Za červenou je to přibližně 42 $^$. A za fialovou – 41 $ ^ $. Paprsky zbývajících barev leží mezi $41^$ a $42^$.
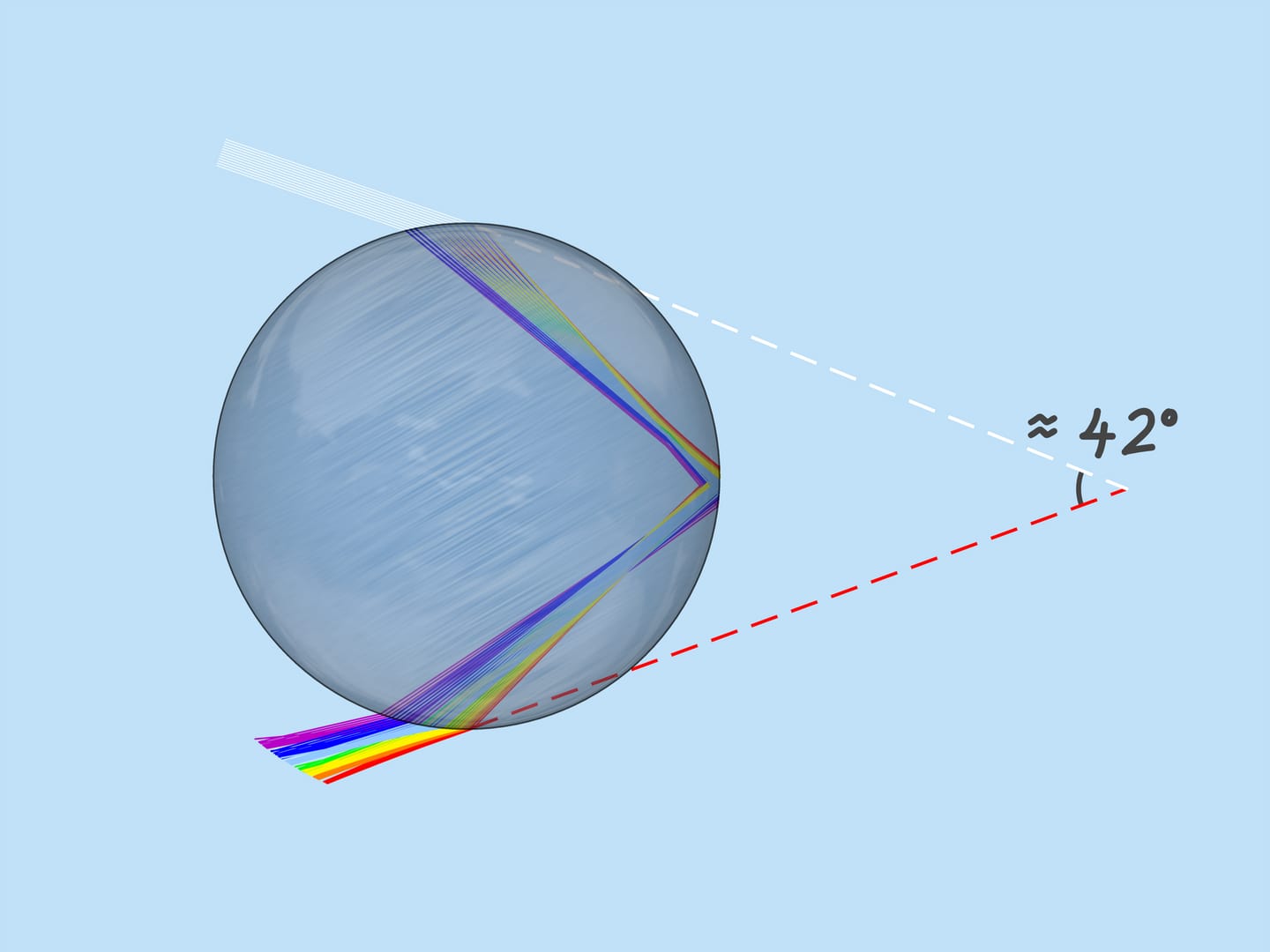
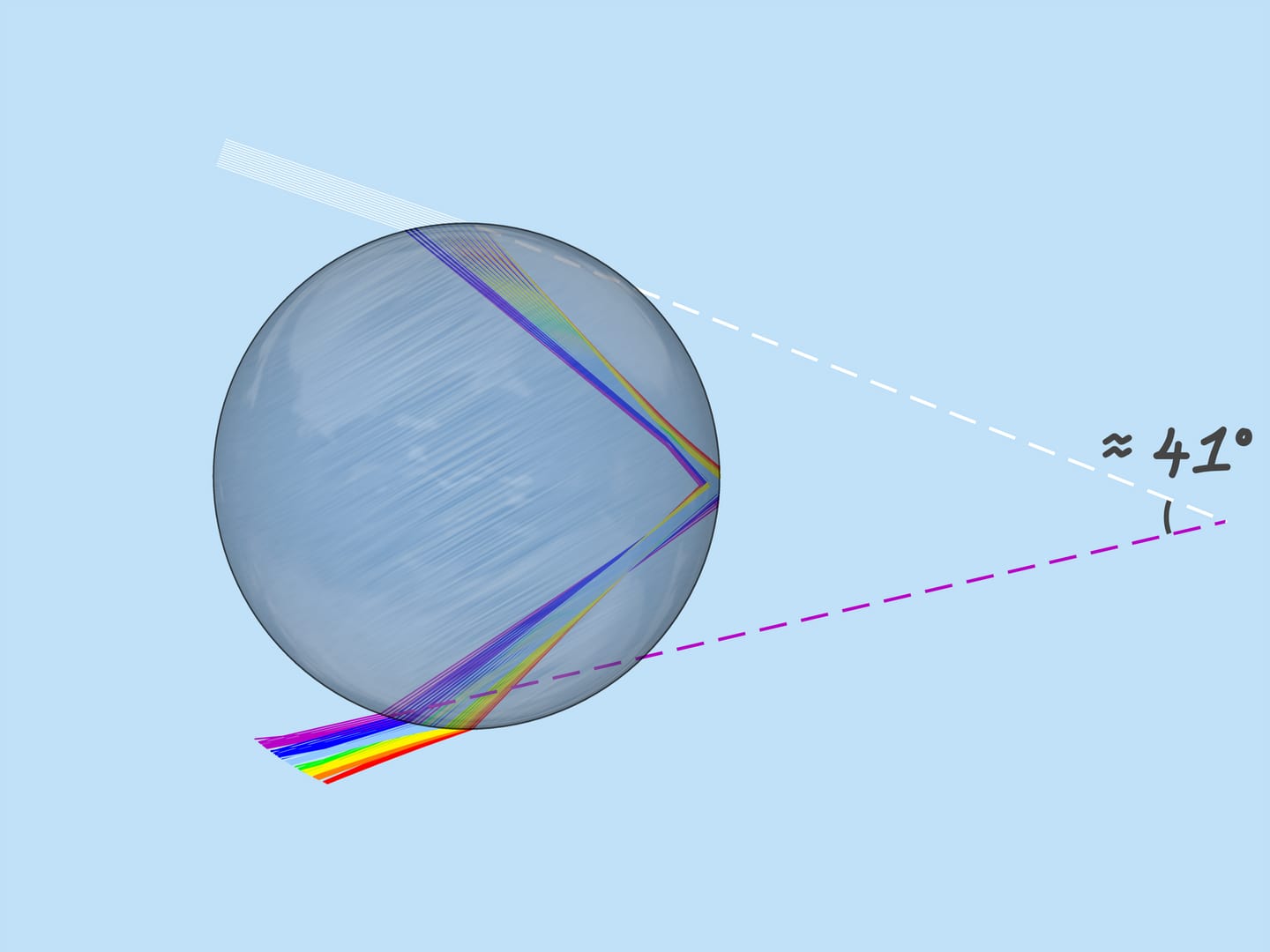
Při pohledu na obrázek průchodu paprsku světla kapkou si všimneme, že pokud například z dané kapky k pozorovateli přijde žlutá barva, pak z této kapky nemůže pocházet žádná jiná barva (červená půjde níže a modrá půjde výše než pozorovatel). Z každé kapky je tedy vidět pouze jedna barva.
Podívejme se nyní na celý soubor dešťových kapek. Jaké kapky se podílejí na vzniku dané barvy duhy? Z výše uvedeného vyplývá, že např. fialovou barvu tvoří ty a jen ty kapky, které leží na přímce svírající úhel $42^$ se slunečními paprsky dopadajícími na zem. To znamená, že fialová barva duhy leží na povrchu kužele s vrcholem u pozorovatele, přičemž osa je pokračováním segmentu „Slunce je oko pozorovatele“ a úhel otevření $42^$. Zbývající barvy také leží na plochách kuželů se stejnou osou a úhly řešení odpovídající těmto barvám.
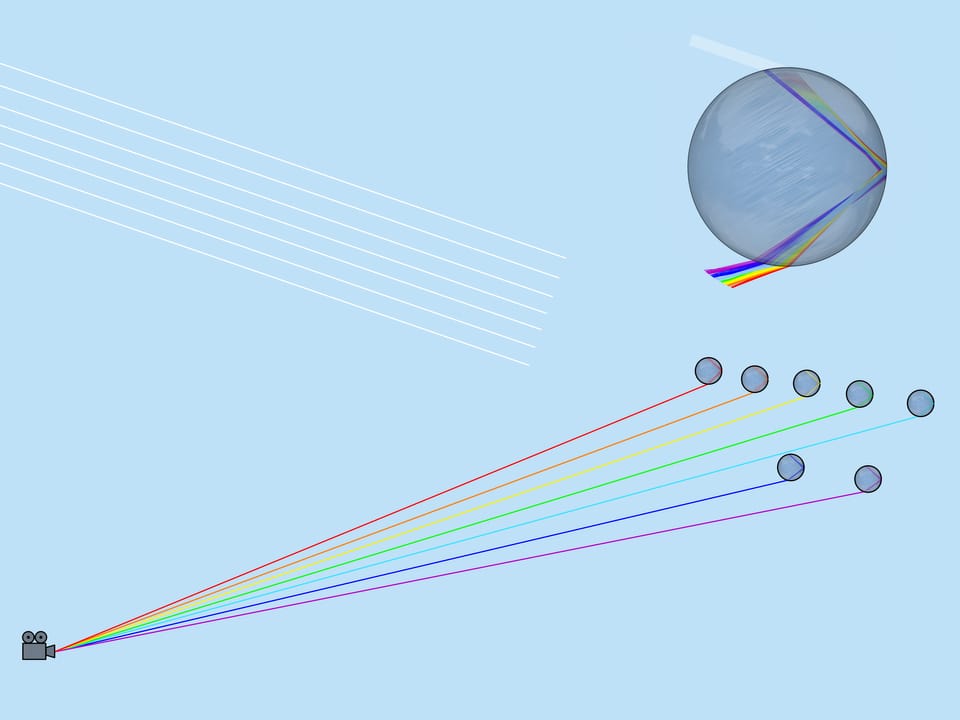
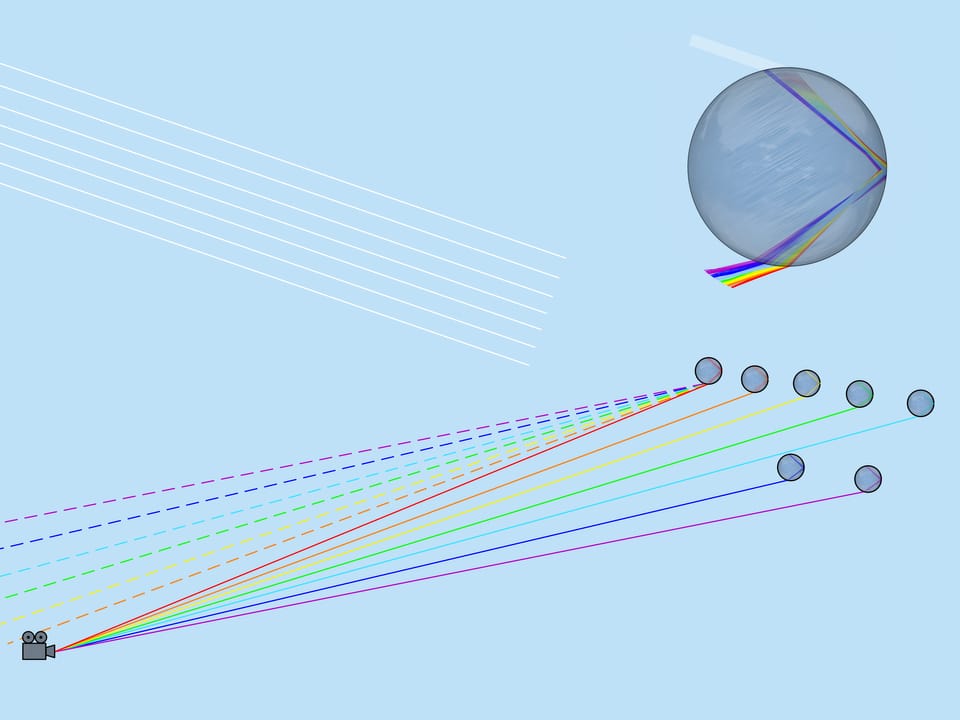
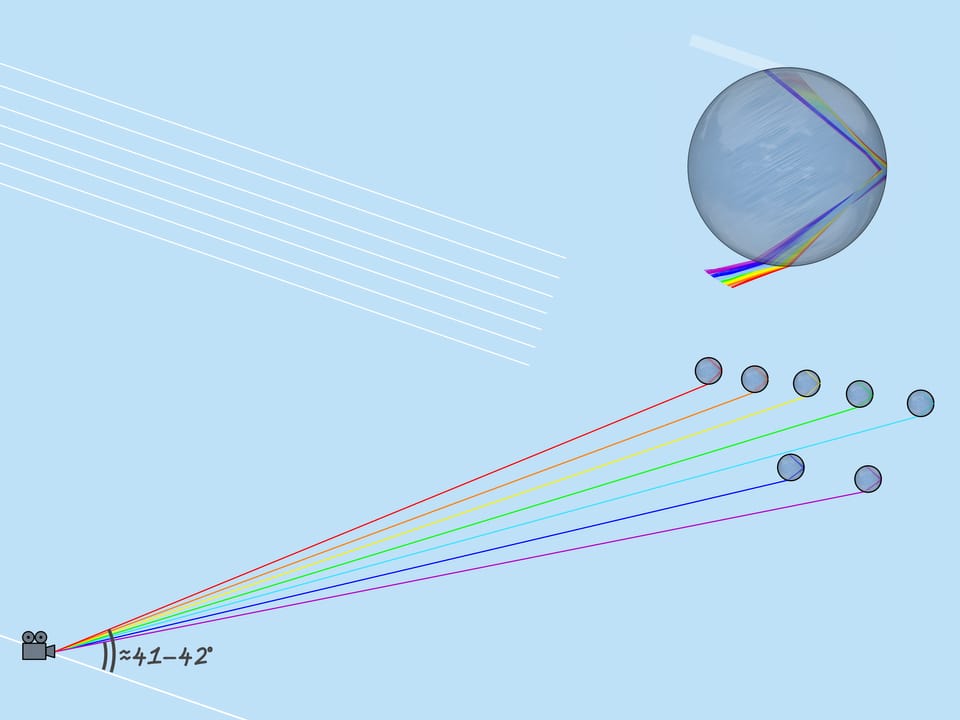
Pokud se pozorovatel podívá na duhu, pak je Slunce za ním. Říká se, že duha je v „antisolárním bodě“. Výška duhy závisí na poloze Slunce. Největší duha nastává, když je Slunce blízko obzoru.
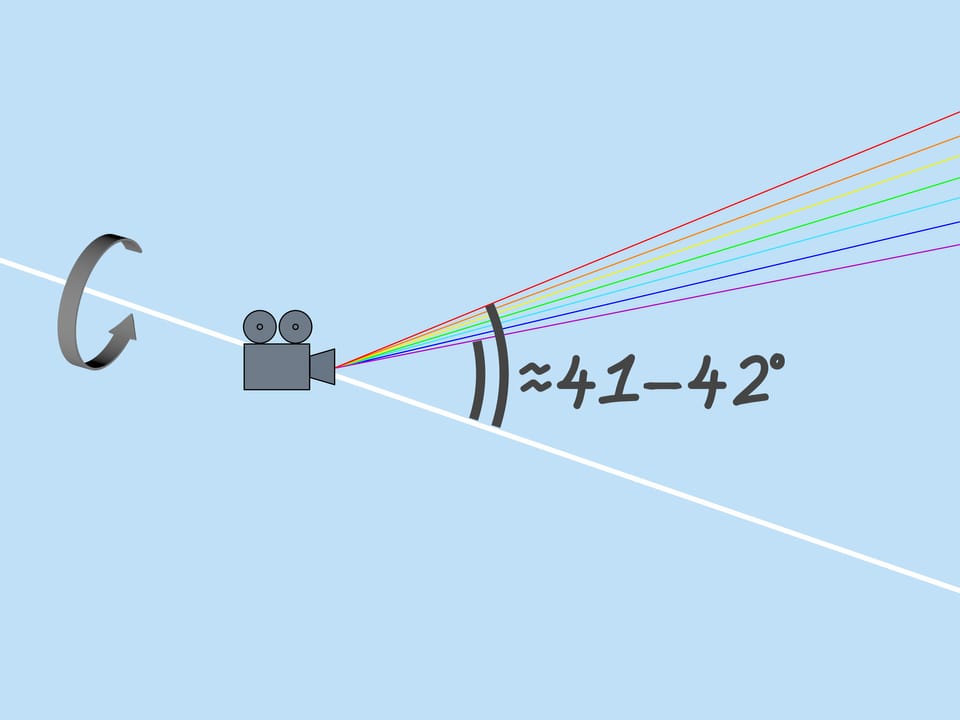

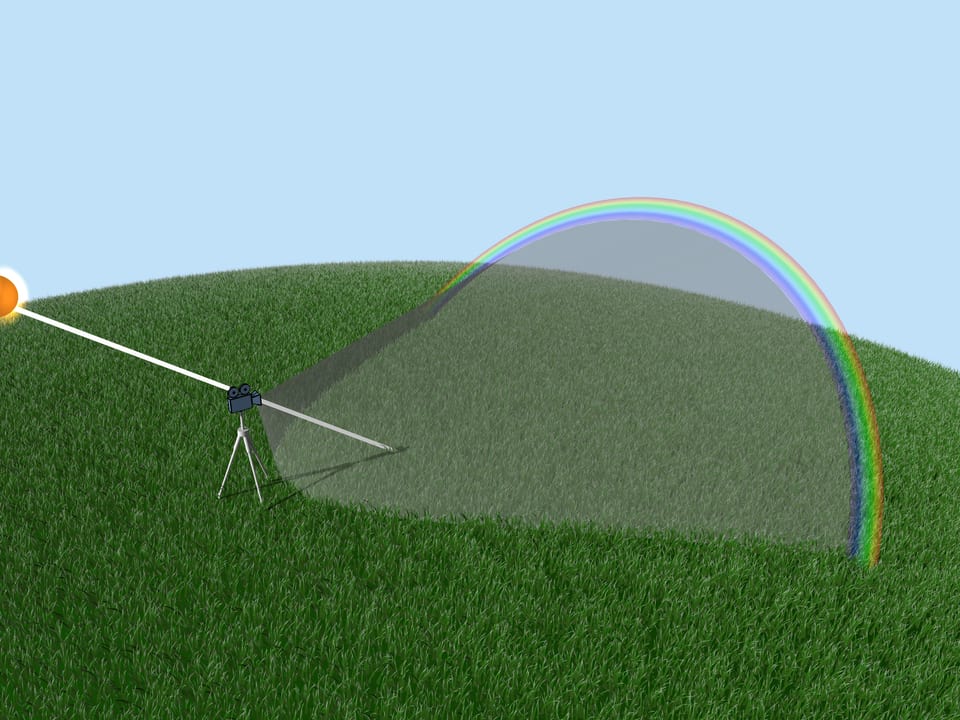
Podívejme se nyní na paprsky Slunce dopadající na spodní část kapky. Vzhledem k symetrii se u nich výše uvedená úvaha může téměř zcela opakovat. Poté však paprsky vycházející z kapky jdou nahoru a pozorovatel ze Země je prostě nevidí. Ale další průchod světelného paprsku kapka po kapce je také možný! Paprsky se mohou dvakrát odrazit od zadní stěny kapky a poté ji opustit.
Tento průchod paprsků dává druhou duhu. Druhá duha je viditelná pod úhlem přibližně $52^$ ke směru Slunce – oko pozorovatele. Je tedy vyšší než první. Vzhledem k tomu, že se paprsky od stěn kapky odrážely dvakrát, pořadí barev v ní je obrácené – červená dole a fialová nahoře.
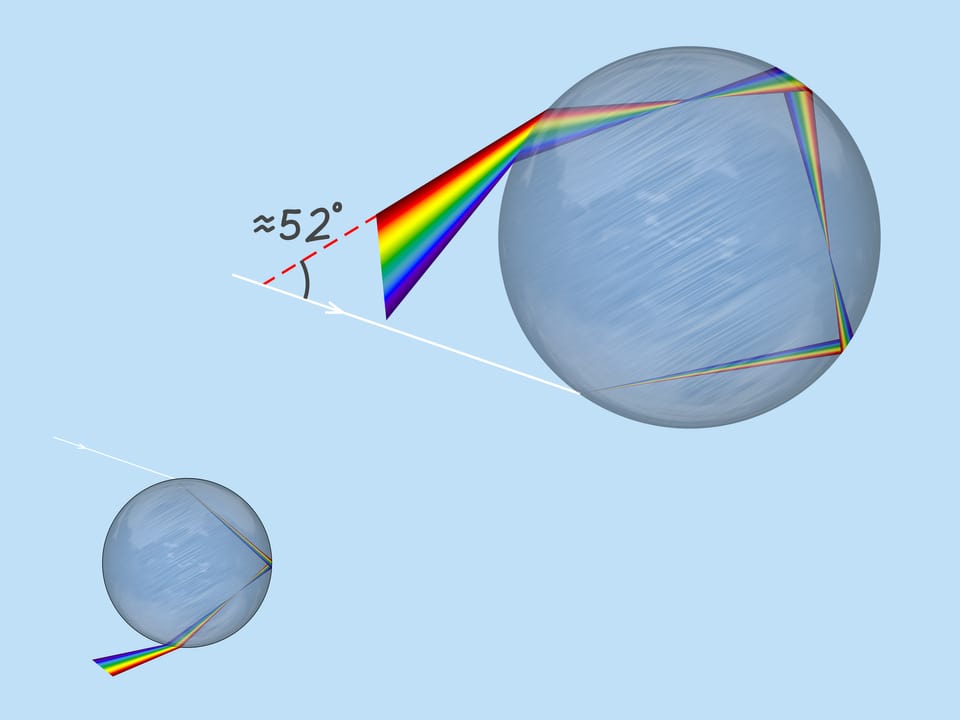
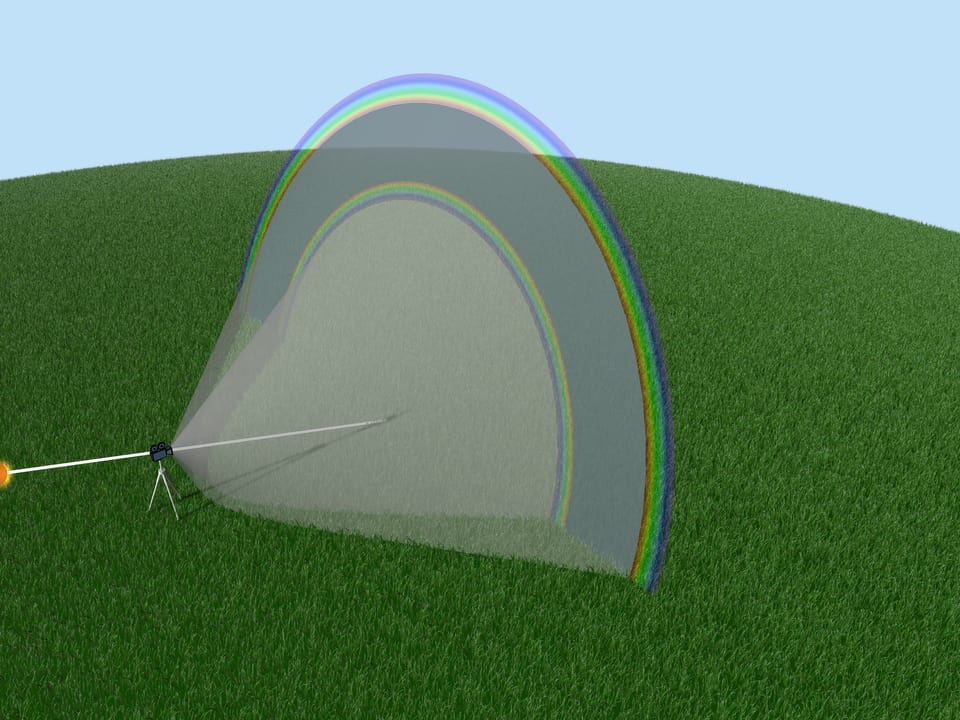

S každým odrazem intenzita světla slábne, takže druhá duha je méně jasná než ta první. Teoreticky existuje třetí duha a duhy vyšších řádů, ale za běžných podmínek nejsou viditelné, protože jsou získány z mnoha odrazů v kapce.
Pozorný člověk si všimne tmavé oblasti oblohy umístěné mezi první a druhou duhou. Faktem je, že po interakci s dešťovými kapkami dorazí k pozorovateli jen malý počet paprsků v úhlech od $41^$ do $52^$. Dalším ne vždy postřehnutým znakem duhy jsou světlé a tmavé pruhy bezprostředně pod fialovým obloukem první duhy. Jejich vysvětlení však přesahuje rámec geometrické optiky.
Pro pozorovatele stojícího na Zemi je nemožné vidět na obloze celý kruh duhy. Úplnou duhu – celý kruh – lze vidět ve šplouchání fontány umístěné nízko nad zemí. A na obloze můžete vidět plnou duhu z letadla.
Literatura
Descartes R. O duze // Descartes R. Úvahy o metodě. S aplikacemi Dioptrie, Meteora, Geometrie / Redakční, překlad, články a komentáře G. G. Slyusareva, A. P. Juškeviče. – M.: Nakladatelství Akademie věd SSSR, 1953. – S. 264-280.
Newton I. Optika aneb Pojednání o odrazech, lomech, ohybech a barvách světla / Překlad ze třetího anglického vydání z roku 1721 s poznámkami S. I. Vavilova. — Druhé vydání / Recenzoval G. S. Landsberg. – M.: GITTL, 1954. – (Klasika přírodních věd. Matematika, mechanika, fyzika, astronomie.)
Arnold V.I. Rainbow // Arnold V.I. Matematické chápání přírody. – M.: MTsNMO, 2010.
Nussenzweig H. Teorie duhy // Pokroky ve fyzikálních vědách. – 1978. – T. 125. – S. 527-547.
Rainbow // Matematická složka / Ed.-comp. N. N. Andreev, S. P. Konovalov, N. M. Panyunin. — Druhé vydání, rozšířené a doplněné. – M.: Matematické studie, 2019. – S. 118-121, 336-338.














