To znamená, že paradox má tento trik: čas, který se měří hodinami, je nahrazen „diskrétním“ časem, měřeným konvergencí Achillovy a želvy v určitých vzdálenostech. Ze skutečnosti, že uplynulo nekonečné množství těchto „diskrétních“ „sekund“, nevyplývá, že podle „skutečných“ hodin uplynulo nekonečné množství času.
Četl jsem zdánlivě vážné články, kde se z tohoto paradoxu vyvozuje závěr, že rozdělení času je limitováno.
Přesně tak. Podle vzhledu. V „diskusních sekcích“ našeho fóra jsou všechna témata na pohled velmi vážná, ale z velké části pramení z autorovy naprosté neznalosti tématu.
| Vážený člen |
Nevím, nevím. Nějaká nepříjemná pachuť z této Zeno aporie stále zůstává.
Zdá se, že říká, že o fyzickém pohybu nelze uvažovat žádným konkrétním způsobem. Účastníci diskuse chtěli ukázat, že by se to dalo myslet i jinak. Ale tato aporie může být formulována tak, že dovednost shrnout použitou geometrickou progresi čtenáři pravděpodobně nepomůže.
Carrolle napsal:
CO ŘEKLA ŽELVA ACHILLESOVI
– Takže naše soutěž skončila? – zeptala se Želva. — Podařilo se vám ještě ujet celou vzdálenost, i když se skládala z nekonečné řady segmentů, a dojet do cíle? Ale abych řekl pravdu, myslel jsem si, že nějaký moudrý muž dokázal, že to nejde.
– Proč ne? – namítl Achilles. – Jak můžeš! Co se dá udělat, už se udělalo! Solvitur ambulando (rozhodnuto mimochodem). Vidíte, délka segmentů se neomezeně zmenšovala a proto.
– Co kdyby se délka segmentů zvýšila neomezeně? – Želva ho přerušila. – Co pak?
“Pak bych neseděl tam, kde sedím,” odpověděl Achilles skromně, “a tou dobou už bys už několikrát obeplul zeměkouli.”
“Lichotíš mi, to znamená, chci říct, že se mi mstíš,” řekla Želva. “Jsem skoro zploštělý: máš velkou váhu.” V čem, v čem, ale v tomhle není chyba. Pokud dovolíte, raději bych vám řekl o soutěži z jiné vzdálenosti. Většina lidí se mylně domnívá, že je v této soutěži dělí do cíle jen dva tři kroky. Ve skutečnosti, abyste se dostali do cíle, musíte překonat nekonečný počet etap a každá následující etapa je delší než ta předchozí.
– S velkým potěšením! – zvolal řecký válečník vroucně a vytáhl z helmy obrovský zápisník a tužku (v těch vzdálených časech mělo kapsy jen velmi málo řeckých válečníků). – Dávám pozor! A mluvte prosím pomaleji: těsnopis ještě nebyl vynalezen!
– Ó, první Euklidův axiom! – řekla zasněně Želva. – Co může být krásnějšího než ty? A dodala a obrátila se k Achilleovi: “Líbí se ti Euclid’s Elements?”
– Blázen! Sotva lze více obdivovat pojednání, které nebude publikováno několik století!
– Báječné! Použijeme úvahy obsažené v prvním axiomu. Potřebujeme pouze dva kroky a z nich vyvozené závěry. Pro usnadnění pozdějších odkazů označme rozsudky jako A, B a Z. Zapište si tedy do sešitu následující:
A) Rovná se témuž jsou si navzájem rovni.
B) Dvě strany tohoto trojúhelníku jsou stejné.
Z) Dvě strany tohoto trojúhelníku jsou si navzájem rovny.
Doufám, že čtenáři a obdivovatelé Euklida budou souhlasit s tím, že závěr Z logicky vyplývá z premis A a B a každý, kdo uzná premisy A a B jako pravdivé, bude muset přijmout závěr Z jako pravdivý. Není to ono?
– Bezpochyby! Každý žák základní školy bude s vaším tvrzením souhlasit – samozřejmě, až když budou školy vynalezeny, a na to si budete muset počkat nějakých dva tisíce let.
– Co když nějaký čtenář neuzná premisy A a B jako pravdivé? Bude stále schopen přijmout závěr Z jako pravdivý?
– Dobře, takový čtenář může být. Zdůvodní něco takového: „Podmíněnou větu „jestliže A a B jsou pravdivé, pak Z je pravdivá“ považuji za pravdivou, ale tvrzení A a B za pravdivé nepovažuji. Takový čtenář by byl moudrý opustit Euklida a věnovat se fotbalu.
— Existuje jiný čtenář, který tvrdí, že uznává pravdivost výroků A a B, ale nepovažuje za pravdivý podmíněný výrok?
– Samozřejmě, že může. Také by pro něj bylo nejlepší dát se na fotbal.
– A žádný z těchto čtenářů by ještě neměl považovat závěr Z za pravdivý z logické nutnosti? – pokračovala Želva.
“Ještě ne,” potvrdil Achilles.
“Pak vás požádám, abyste mě považoval za zástupce druhé kategorie čtenářů a pomocí logických argumentů mě donutil přiznat pravdivost závěru Z.”
“Želva hrající fotbal. ” začal Achilles, ale želva ho spěšně přerušila:
– . byl by to samozřejmě neobvyklý pohled. Neuhýbejme od hlavního bodu. Nejdřív pravda závěru Z, pak fotbal!
“Takže, jestli tomu dobře rozumím, je mou zodpovědností tě donutit přiznat pravdu úsudku Z,” řekl Achilles zamyšleně. — Pozice, kterou zaujmete, se scvrkne na následující. Přijímáte pravdivost výroků A a B, ale nepřijímáte pravdivost podmíněného výroku.
“Bude pro nás pohodlnější mluvit, když označíme podmíněný návrh C,” navrhla Želva.
“Dobře,” souhlasil Achilles. – Takže neznáte pravdivost tvrzení C:
“Pokud A a B jsou pravdivé, pak Z musí být pravdivé.”
“Toto je moje současné postavení,” potvrdila Želva.
– Pak vás musím požádat, abyste přiznal pravdu C.
“Udělám to,” řekla Želva, “jakmile si zapíšeš návrh C do sešitu.” Má už nějaké záznamy?
“Jen pár poznámek,” odpověděl Achilles a horečně listoval stránkami, “o různých památných událostech. o bitvách, ve kterých jsem se vyznamenal.”
– Vidím spoustu prázdných stránek! – želva radostně zvolala: “Budeme je všechny potřebovat.” (Achilles se otřásl hrůzou.) Napište prosím:
A) Rovná se témuž jsou si navzájem rovni.
B) Dvě strany tohoto trojúhelníku jsou stejné.
C) Jsou-li A a B pravdivé, pak Z musí platit.
Z ) Dvě strany tohoto trojúhelníku jsou si navzájem rovny.
“Měl jsi označit poslední rozsudek písmenem D, ne Z,” řekl Achilles. – Přichází hned po prvních třech rozsudcích. Pokud považujete výroky A, B a C za pravdivé, pak vám nezbývá nic jiného, než pravdivost výroku přiznat.
– Proč si myslíš, že musím uznat pravdivost rozsudku Z?
– Protože to logicky vyplývá z A, B a C. Jsou-li A, B a C pravdivé, pak Z musí platit. Doufám, že proti tomu nebudete mít námitky?
“Pokud jsou A, B a C pravdivé, pak Z musí být pravdivé. ” opakovala želva zamyšleně. – Ale to je nový podmíněný návrh! A pokud nejsem přesvědčen o jeho pravdivosti, pak mohu považovat A, B a C za pravdivé, ale stejně neuznávám Z jako pravdivé. Že jo?
“To je pravda,” potvrdil hrdina, “i když musím říci, že tento druh tvrdohlavosti vypadá velmi zvláštně.” Protože je to však také možné, jsem nucen vás požádat, abyste uznal pravdivost dalšího podmíněného návrhu.
– S radostí! Snadno připustím pravdivost tohoto úsudku, jakmile si jej zapíšete do sešitu. Označme to D. Tak,
D) “Pokud jsou A, B a C pravdivé, pak Z musí být pravdivé.”
– Natočeno! “ zvolal radostně Achilles a jeho tužka rychle přejela po papíru. – Konečně jsme se dostali do cíle naší logické soutěže! Nyní, když jste rozpoznali pravdivost úsudků A, B, C a D, samozřejmě uznáváte pravdu závěru Z!
– Je to opravdu nutné? “ zeptala se Turtle s nevinným pohledem. – Zkusme na to přijít. Přijímám pravdivost tvrzení A, B, C a D. Ale co když stále neuznávám pravdivost závěru Z?
“Potom tě Logic vezme pod krkem a donutí tě to udělat!” – vítězoslavně odpověděl Achilles. – Logika vám řekne: „Nemáš jinou možnost. Jakmile přijmete pravdivost výroků A, B, C a D, musíte přijmout pravdivost závěru Z! – Takže, jak vidíte, není jiné východisko.
“To, co mi řekl Logic, by se mělo zapsat,” řekla Želva. “Zapište si do sešitu prosím podmíněný návrh, který označíme E:
E) “Pokud jsou A, B, C a D pravdivé, pak Z musí platit.”
Dokud nebudu souhlasit s přijetím pravdivosti výroku E, nemusím přijmout pravdivost výroku Z, takže jednoduše potřebujeme rozsudek E. Souhlasíš?
“Souhlasím,” odpověděl Achilles s nádechem smutku v hlase.
V tuto chvíli naléhavé záležitosti v bance donutily vypravěče opustit šťastný pár. Jen o několik měsíců později náhodou znovu prošel kolem místa, kde si Achilles a Želva povídali. Achilles stále seděl na zádech trpělivé Želvy a něco psal do téměř plného sešitu.
Když se přiblížil, vypravěč slyšel, jak želva říká:
— Zapsali jste si poslední podmíněný návrh? Pokud jsem neztratil počet, měla by to být první tisícovka. Ještě pár milionů zbývá. Chci vás požádat o osobní laskavost. Nevadilo by vám, kdybych vám přečetl krátké básně své vlastní skladby? Jako polehčující okolnost vás žádám, abyste měli na paměti kontroverzi, kterou náš rozhovor vyvolá mezi logiky devatenáctého století.
– Přečtěte si cokoli! – zvolal zoufale nešťastný válečník a zakryl si obličej rukama. A želva recitovala:
Achillova pata
Všechny naznačují špatnou věc.
Lebka – ach! – praská myšlenkami:
Achilles má slabou mysl!
Zajímalo by mě, co si o této formulaci myslí účastníci?
Řekl bych, že problém podobný Zenónovi se nevyskytuje ve vztahu k fyzickému pohybu, ale k pohybu myšlení nebo tak něco. Zdá se, že tento myšlenkový pohyb lze znázornit i nějakým jiným způsobem, ale tímto jiným zobrazením nebude zachována tak důležitá charakteristika, jako je „důkaz“. „Prostor myšlenek“ není měřitelný pohodlným způsobem, abych tak řekl.
| Vážený člen |
V tomto případě lze absolutně jakýkoli výrok považovat za aporii. Zeno tedy opět nepřišel s ničím zajímavým.
18.02.2008, 06: 40
Citace:
Jak ukazuje moje osobní zkušenost, Zenoova aporie je ideální zkouškou pro samostatné myšlení. Navíc je to právě ten test, ve kterém mohou lidé s nejčestnějšími tituly selhat. Navíc to zpravidla neskládají držitelé technických diplomů a titulů, kteří Zenóna nazývají „sofistou“. Neboť „technici“ jsou zvyklí pracovat s jasnými definicemi, zavedenou formalizací atd., a Zenoova aporie je tou velmi epistemologickou noční můrou, která se dívá na samotný kořen a zpochybňuje jakoukoli formalizaci a jakékoli termíny. Vyžadují myšlení nezatížené dogmaty, tedy myšlení samostatné. Ukazují rozdíl mezi znalostmi a inteligencí, erudicí a inteligencí.
Zenonova aporie dodnes nenašla uspokojivé řešení. Navíc moderní publikace, na rozdíl od sovětských, s tím souhlasí: „A[poria] jsou nyní uznávány jako skutečné paradoxy spojené zejména s popisem pohybu“[2]. Jak uvidíte později, všechny tzv. „rezoluce“ aporií představují logický omyl ignorantia elenchi spočívající v tom, že dokazovaná teze není ta, kterou je třeba dokazovat
Jak správně poznamenal William James, kritika Zenónových úvah, že má-li nekonečná řada složená z časových intervalů konečný součet, pak Achilles musí předběhnout želvu, „zcela míjí cíl. Zenón by docela ochotně souhlasil s tím, že pokud lze želvu vůbec předjet, pak ji lze předjet třeba za dvacet sekund; ale přesto by trval na tom, že je nemožné ji vůbec dohnat“[5]. Skutečně, ze skutečnosti, že celý časový interval, který je mu pro tento akt přidělen, má konečnou míru, automaticky nevyplývá, že může tuto sekvenci skutečně vyčerpat.
Konečně lze změnit formulaci aporie, aniž by se změnila podstata jejího problému: „Nejrychlejší běžec nebude moci dohnat nejpomalejšího (ač se nepřestane hýbat), protože ten, kdo dohání, musí nejprve dosáhnou místa, odkud se běžec posunul, takže ten pomalejší půjde vpřed.“
Přitom výše uvedená úvaha, že součet nekonečného počtu časových intervalů přesto konverguje, a dává tak konečný časový úsek, absolutně neovlivňuje jeden v podstatě paradoxní bod, totiž paradox, že určitá nekonečná posloupnost po sobě jdoucích po sobě událostí musí být ve skutečnosti stále dokončen sled, jehož dokončení si (nejen fyzicky, ale alespoň principiálně) ani neumíme představit. Aporia si neklade otázku limity a jejího výpočtu, aporia se ptá: jak je této hranice v principu možné dosáhnout?
Podstata problému spočívá v integraci nekonečného počtu částí a matematická analýza uvažuje o diferenciaci již definovaného, a tedy aktualizovaného nekonečna: celý přírůstek již byl dán a zbývá pouze rozdělit – a, v případě infinitezimálních veličin již není aktuální, ale potenciálně! (o tom si povíme později) – je rozdělena na kousky; zatímco Zenón si klade otázku, jak může být tento celek složen z takových částí (a teprve potom se to snažit rozdělit)? Ukazuje se, že samotné řešení je možné pouze tehdy, když je proces dokončen, to znamená, že je ve skutečnosti možné pouze se skutečným nekonečnem, a to není nic jiného než „rozlišení“ aporie postulováním přítomnosti řešení. . Podle Zenónových obecných argumentů nemůžeme získat ani Δs ani Δt, a proto se vůbec nemůžeme uchýlit k matematické analýze. To znamená, že „rozlišení“ aporie pomocí matematické analýzy není nic jiného než logická chyba circulus vitiosus.
Neztrácejme čas a zpomalme Achilla, který je připraven předjet zákeřnou želvu.
Dáno: Rychlost želvy je Vh, rychlost Achilla je Va, vzdálenost mezi nimi je L.
Najít: čas přiblížení je T, za předpokladu, že se rovná součtu časů, za které urazí polovinu zbývající vzdálenosti mezi nimi.
T = (1/2)*L/(Va-Vch) + (1/2)^2*L/(Va-Vch)+….+ (1/2)^n*L/(Va-Vch) s n inklinujícím k nekonečnu, kde ^n znamená zvýšení na mocninu n.
Zjednodušme výraz
T = (L/(Va-Vch))*(SOUČET od 1 do nekonečna řady (1/2)^n)
Chcete-li najít součet řady, můžete použít některou z matematických stránek (soustřeďujících výdobytky moderní matematiky), například math24.biz/sum.
Zde se každý může zúčastnit matematické expozice Zeno.
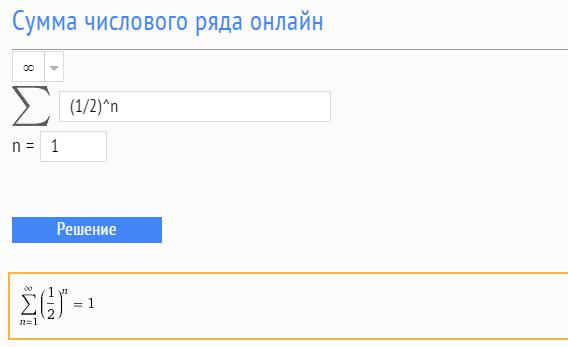
Zde (viz obrázek) je třeba vzorec řady zapsat jako (1/2)^n a nastavit počáteční
hodnota n=1. Horní hranice částky je nastavena na děsivou hodnotu „+ nekonečno“. Jako na obrázku.
Jediné, co musíte udělat, je stisknout tlačítko (Solution nebo Enter), 2-3 sekundy a odpověď na Zenoovu otázku, starou jako svět, je připravena. Součet této řady je přesně roven 1.
Pak je čas se přiblížit
T = L/(Va-Vch).
Je konečný a předvídatelný.Z hlediska matematiky bylo paradoxem, že Zenón prezentoval obvyklou jednotku ve formě, která byla pro jeho dobu neřešitelná.
Velký mudrc Zeno samozřejmě může říci: Tisíc let jste přemýšleli o jedné verzi problému, ale co kdyby se Achilles pokaždé přiblížil na 2/3 vzdálenosti nebo jakékoli jiné číslo menší než jedna?
Odpověď na tuto otázku je již také připravena, protože matematika neřeší konkrétní problémy, vždy se snaží najít obecné řešení pro mnoho podobných problémů. V tomto případě máme co do činění s nekonečně klesajícími geometrickými posloupnostmi, u kterých stačí zadat první prvek a jmenovatel geometrické posloupnosti (v absolutní hodnotě menší než jedna).
Označme část cesty, kterou Achilles pokaždé změří od zbytku, jako k/m, kde k a m jsou libovolná kladná celá čísla a k < m. Obecné řešení bude vypadat takto:
T = (L/( Va-Vch))*(k/m)*(SOUČET od 1 do nekonečna řady ((m-k)/m)^(n-1) )
Ve skutečnosti je nekonečně klesající geometrická progrese sama o sobě následující:
SOUČET od 1 do nekonečna řady ((m-k)/m)^(n-1)
Obecné řešení pro nalezení součtu (S) nekonečně klesající geometrické posloupnosti:
S = b1/(1-q)
kde b1 je první člen progrese a q je jmenovatel progrese.
b1 je nalezeno pro n=1.
b1 = ((m-k)/m)^0 = 1
q se v našem případě rovná (m-k)/m
pak:
S = 1/(1 – ((m-k)/m)) = m/k
T = (L/( Va-Vch))*(k/m)*(m/k) = L/(Va-Vch)
Ve výsledku jsme dostali stejné známé (opakovaně přešlapované) řešení pro rovnoměrný přímočarý pohyb. Výsledek je určen pouze rychlostí přiblížení Achilla a želvy a nijak nezávisí na mazaném uvažování Zenóna, který je sleduje.
Zenónův paradox je vyřešen. Achilles nevyhnutelně dohoní zrádnou želvu. Ve skutečnosti už želva není zákeřná. Je to obyčejné, v některých ohledech dokonce roztomilé stvoření.
Je ale Zeno poražen? Připomeňme si, co vlastně chtěl Zeno dokázat svým paradoxem:
Že Achilles želvu nikdy nedohoní?
Nebo že segment nemůže sestávat z nekonečně malých částí?
Zeno přišel se svým paradoxem a pokusil se ukázat absurditu dělení segmentu na nekonečně malé části. Zeno se pokusil dokázat konverzací, že každý segment se skládá z konečného počtu částí a že neexistuje nic takového jako nekonečná malá. Co dělat, mudrci nikdy neměli rádi nekonečna.
Zenón nebyl zapomenut, navíc stál v čele bitvy vědeckých teorií. Na jedné straně kvantová fyzika, která úspěšně aplikovala kvantovou teorii pole na elektromagnetické, silné a elektroslabé interakce, si klade za cíl gravitační pole kvantovat. Na druhou stranu gravitační pole je, i když gravitací zakřivené, spojitý prostor obecné teorie relativity.
Přední linie leží v extrémně krátkých vzdálenostech v řádu Planckovy délky (10 minus 33 metrů). Planckova konstanta je „docela šíleným“ výtvorem kvantové fyziky. Frontová linie přitom prochází podmínkami extrémní komprese černých děr – onoho ponurého požírače hvězd, který předpovídá obecná teorie relativity. A bez ohledu na to, jak malá je hranice, Achilles ji bude muset překročit.
V důsledku bitvy vědeckých teorií, která překročila hranici století, se objevily teorie kvantové gravitace, které se snaží fyzikové vyzkoušet. V roce 2020 vyšel překlad knihy „Unreal Reality“ od jednoho ze zakladatelů teorie smyčkové kvantové gravitace Carla Rovelliho. Zde je jeho závěr ohledně osudu nešťastného pronásledovatele želvy Zeno:
„Achilles nemusí dělat nekonečné množství kroků, aby želvu dohnal, protože ve vesmíru, který se skládá ze zrn konečné velikosti, nekonečně malé kroky neexistují. Hrdina se bude k želvě přibližovat stále blíž, až ji nakonec jedním kvantovým skokem předběhne.“
Toto je v tuto chvíli dramatický výsledek Zenónova paradoxu.
PS
Zde jsou dvě Zenoovy aporie spojeny do jednoho paradoxu: „Dichotomie“ a „Achilles a želva“. Existují pouze tři parametry:
Achillova rychlost,
rychlost želvy,
poměr, ve kterém je segment k/m rozdělen.
Pro „dichotomii“: Achillova rychlost = V, rychlost želvy = 0, k/m = 1/2;.
Pro “Achilles a želva”: Rychlost Achilla = 10V, rychlost želvy = V, k/m = 9/10. Úvodní slovo aporie „předpokládej“ také implikuje jakékoli jiné dělení segmentu.
Aporie a paradox mají společné to, že logicky správné uvažování vede k logickému rozporu. Paradoxy nepochybně naznačují chybu ve výchozích bodech nebo v řetězci logického uvažování. O logice jako primární vědě, o aplikaci logiky k řešení kanonických problémů a populárních hádankách si můžete přečíst zde: „Primární věda o logice“ http://proza.ru/2020/05/03/1236
© Copyright: Kuznetsov Sergey Grig, 2013
Osvědčení o zveřejnění č. 213011501005
„Carlo Rovelli. Zde je jeho závěr ohledně osudu nešťastného pronásledovatele želvy Zeno:
„Achilles nemusí dělat nekonečné množství kroků, aby želvu dohnal, protože ve vesmíru, který se skládá ze zrn konečné velikosti. “
Je „materiálnost“ („zrnitost“) prostoru prokázaným faktem, nebo je to jen názor Rovelliho „a těch, kteří se k němu přidali“?
Děkuji za vaši práci.
Tato práce byla napsána pro 5 recenzí, zde se zobrazuje poslední, ostatní jsou v úplném seznamu.
Portál Proza.ru poskytuje autorům možnost volně publikovat svá literární díla na internetu na základě uživatelské smlouvy. Veškerá autorská práva k dílům náleží autorům a jsou chráněna zákonem. Přetisk díla je možný pouze se souhlasem jeho autora, na kterého se můžete odkázat na jeho autorské stránce. Za texty děl odpovídají autoři samostatně na základě pravidel publikování a legislativy Ruské federace. Údaje uživatelů jsou zpracovávány na základě Zásad zpracování osobních údajů. Můžete si také prohlédnout podrobnější informace o portálu a kontaktovat administraci.
Denní návštěvnost portálu Proza.ru je asi 100 tisíc návštěvníků, kteří si celkem prohlédnou více než půl milionu stránek podle počítadla návštěvnosti, které se nachází vpravo od tohoto textu. Každý sloupec obsahuje dvě čísla: počet zobrazení a počet návštěvníků.
© Všechna práva vyhrazena autorům, 2000-2023. Portál funguje pod záštitou Ruského svazu spisovatelů. 18+
















